Η δομή της επανάληψης.
Η διαδικασία της επανάληψης είναι ιδιαίτερα συχνή, σε πλήθος προβλημάτων στα οποία θα πρέπει να επαναληφθούν οι ίδιες ακριβώς εντολές, πολλές φορές προκειμένου να γίνει εισαγωγή των δεδομένων, η επεξεργασία τους ή ακόμη και η εμφάνιση των αποτελεσμάτων. Σε τέτοιες περιπτώσεις είναι πολύ πιο εύκολο να μάθουμε πώς επαναλαμβάνονται στον αλγόριθμό μας οι εντολές αυτές παρά να τις γράψουμε πολλές φορές!
Ας σκεφτούμε κάτι απλό για να κατανοήσουμε την ανάγκη της χρήσης των επαναληπτικών διαδικασιών, έστω λοιπόν ότι θέλουμε να φτιάξουμε ένα πρόγραμμα το οποίο να δέχεται σαν είσοδο πενήντα διαφορετικούς αριθμούς ( οι οποίοι θα είναι επιλογές του χρήστη ),και στη συνέχεια θα υπολογίζει και θα εμφανίζει το μέσο όρο των αριθμών αυτών. Σε αυτή τη περίπτωση αν επιχειρήσουμε να δώσουμε μια λύση με βάση αυτά που γνωρίζουμε μέχρι τώρα θα δούμε ότι πρέπει να επαναλάβουμε πενήντα φορές ( ! ) τις εντολές εισόδου για να διαβαστούν και οι πενήντα αριθμοί καθώς επίσης άλλες τόσες για να προσθέτουμε κάθε αριθμό προκειμένου να υπολογίσουμε το συνολικό άθροισμα! Δεν είναι δύσκολο να καταλάβουμε ότι μια τέτοια αντιμετώπιση θα έκανε την επίλυση του συγκεκριμένου προβλήματος μια ιδιαίτερα επίπονη διαδικασία με πάρα πολύ γράψιμο, δίχως ουσιαστικό λόγο.
Προκειμένου να αντιμετωπίσουμε τέτοιου είδους προβλήματα θα μελετήσουμε τρεις διαφορετικές δομές επανάληψης, την δομή επανάληψης «ΓΙΑ…ΑΠΟ…ΜΕΧΡΙ…» ή πιο απλά «για», την δομή επανάληψης «ΟΣΟ…ΕΠΑΝΑΛΑΒΕ» και την δομή επανάληψης «ΑΡΧΗ_ΕΠΑΝΑΛΗΨΗΣ…ΜΕΧΡΙΣ_ΟΤΟΥ».
Στη συνέχεια θα δούμε πως συντάσσεται κάθε μια από τις παραπάνω δομές καθώς επίσης και πότε χρησιμοποιούμε την κάθε δομή έτσι ώστε να έχουμε το καλύτερο δυνατό αποτέλεσμα.
Ας σκεφτούμε κάτι απλό για να κατανοήσουμε την ανάγκη της χρήσης των επαναληπτικών διαδικασιών, έστω λοιπόν ότι θέλουμε να φτιάξουμε ένα πρόγραμμα το οποίο να δέχεται σαν είσοδο πενήντα διαφορετικούς αριθμούς ( οι οποίοι θα είναι επιλογές του χρήστη ),και στη συνέχεια θα υπολογίζει και θα εμφανίζει το μέσο όρο των αριθμών αυτών. Σε αυτή τη περίπτωση αν επιχειρήσουμε να δώσουμε μια λύση με βάση αυτά που γνωρίζουμε μέχρι τώρα θα δούμε ότι πρέπει να επαναλάβουμε πενήντα φορές ( ! ) τις εντολές εισόδου για να διαβαστούν και οι πενήντα αριθμοί καθώς επίσης άλλες τόσες για να προσθέτουμε κάθε αριθμό προκειμένου να υπολογίσουμε το συνολικό άθροισμα! Δεν είναι δύσκολο να καταλάβουμε ότι μια τέτοια αντιμετώπιση θα έκανε την επίλυση του συγκεκριμένου προβλήματος μια ιδιαίτερα επίπονη διαδικασία με πάρα πολύ γράψιμο, δίχως ουσιαστικό λόγο.
Προκειμένου να αντιμετωπίσουμε τέτοιου είδους προβλήματα θα μελετήσουμε τρεις διαφορετικές δομές επανάληψης, την δομή επανάληψης «ΓΙΑ…ΑΠΟ…ΜΕΧΡΙ…» ή πιο απλά «για», την δομή επανάληψης «ΟΣΟ…ΕΠΑΝΑΛΑΒΕ» και την δομή επανάληψης «ΑΡΧΗ_ΕΠΑΝΑΛΗΨΗΣ…ΜΕΧΡΙΣ_ΟΤΟΥ».
Στη συνέχεια θα δούμε πως συντάσσεται κάθε μια από τις παραπάνω δομές καθώς επίσης και πότε χρησιμοποιούμε την κάθε δομή έτσι ώστε να έχουμε το καλύτερο δυνατό αποτέλεσμα.
Η Δομή Επανάληψης "ΓΙΑ"
Στις περιπτώσεις εκείνες που γνωρίζουμε από την αρχή πόσες επαναλήψεις θα πραγματοποιηθούν στην άσκησή μας, μπορούμε να χρησιμοποιήσουμε τη δομή επανάληψης «ΓΙΑ…». Αυτός είναι και ο περιορισμός που έχουμε σε αυτή τη δομή ,ότι δηλαδή αν δεν γνωρίζουμε πόσες φορές θα πραγματοποιηθεί η επανάληψη δεν μπορούμε να χρησιμοποιήσουμε τη δομή επανάληψης «ΓΙΑ…», ο λόγος θα γίνει κατανοητός αν μελετήσουμε το πώς συντάσσεται η δομή αυτή:
Η γενική μορφή σύνταξης της επανάληψης «ΓΙΑ…ΑΠΟ…ΜΕΧΡΙ…» είναι η εξής :
ΓΙΑ ( ΜΕΤΡΗΤΗΣ) ΑΠΟ (ΑΡΧΙΚΗ ΤΙΜΗ) ΜΕΧΡΙ (ΤΕΛΙΚΗ ΤΙΜΗ) ΜΕ_ΒΗΜΑ (ΒΗΜΑ)
{ Ομάδα εντολών }
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
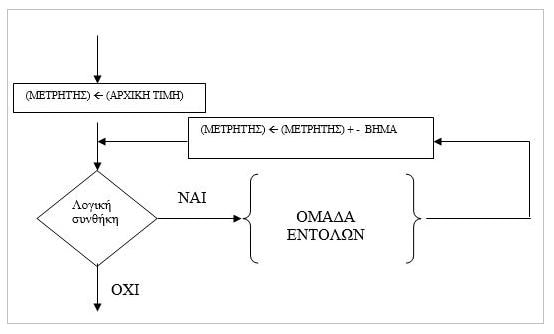
Επίσης η διαγραμματική αναπαράσταση αυτής της επαναληπτικής δομής έχει την παρακάτω γενική μορφή :
Η γενική μορφή σύνταξης της επανάληψης «ΓΙΑ…ΑΠΟ…ΜΕΧΡΙ…» είναι η εξής :
ΓΙΑ ( ΜΕΤΡΗΤΗΣ) ΑΠΟ (ΑΡΧΙΚΗ ΤΙΜΗ) ΜΕΧΡΙ (ΤΕΛΙΚΗ ΤΙΜΗ) ΜΕ_ΒΗΜΑ (ΒΗΜΑ)
{ Ομάδα εντολών }
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
Επίσης η διαγραμματική αναπαράσταση αυτής της επαναληπτικής δομής έχει την παρακάτω γενική μορφή :
Επεξήγηση της δομής επανάληψης « για »
Βασικό στοιχείο της δομής αυτής είναι ο μετρητής. Ο μετρητής είναι μια ειδική μεταβλητή η οποία καθορίζει πόσες φορές θα πραγματοποιηθεί η επανάληψη και ποτέ θα τερματιστεί. Συνήθως ο μετρητής συμβολίζεται με το γράμμα i ή j .
Ως αρχική τιμή, ορίζουμε την τιμή από την οποία θα ξεκινήσει ο μετρητής.
Η τελική τιμή είναι η τιμή εκείνη την οποία όταν ξεπεράσει ο μετρητής, η επανάληψη τερματίζεται. Εδώ μπορεί να έχουμε δυο περιπτώσεις, η πρώτη είναι να έχουμε αρχική τιμή μικρότερη από την τελική και η δεύτερη να έχουμε αρχική τιμή μεγαλύτερη από την τελική. Στην πρώτη περίπτωση για να τερματιστεί η επαναληπτική δομή θα πρέπει ο μετρητής να πάρει τιμή μεγαλύτερη από την τελική, ενώ στη δεύτερη, για να τερματιστεί η επανάληψη θα πρέπει ο μετρητής να πάρει τιμή μικρότερη από την τελική. Προσοχή , όταν ο μετρητής έχει τιμή ίση με την τελική, η επανάληψη εκτελείται για ακόμη μια φορά.
Το βήμα περιγράφει πόσο μεταβάλλεται ο μετρητής κάθε φορά που εκτελείται μια επανάληψη. Το βήμα μπορεί να έχει θετική τιμή (όταν η αρχική τιμή είναι μικρότερη της τελικής), ή αρνητική τιμή (όταν η αρχική τιμή είναι μεγαλύτερη από την τελική).
Βέβαια η δομή αυτή μπορεί να μην εκτελεστεί καμία φορά, για παράδειγμα αν η αρχική τιμή είναι μικρότερη της τελικής και το βήμα αρνητικό,
πχ: ΓΙΑ i ΑΠΟ 1 ΜΕΧΡΙ 100 ΜΕ_ΒΗΜΑ –2
Μελέτη λειτουργίας της επαναληπτικής δομής «ΓΙΑ» :
- Αρχικά εκχωρείται στο μετρητή η αρχική τιμή,
- Ο μετρητής συγκρίνεται με την τελική τιμή, και αν η λογική συνθήκη είναι αληθής τότε μόνο συνεχίζεται η εκτέλεση των εντολών της επανάληψης.
- Αφού εκτελεστεί η ομάδα εντολών, πριν τελειώσει η επανάληψη ο μετρητής μεταβάλλεται (αυξάνεται ή μειώνεται, αναλόγως του βήματος)
- Ο μετρητής συγκρίνεται πάλι με την τελική τιμή και η επανάληψη θα πραγματοποιηθεί ξανά μόνο στην περίπτωση που η λογική συνθήκη είναι αληθής.
- Όταν ο μετρητής ξεπεράσει την τελική τιμή (αν έχουμε θετικό βήμα ) ή αντίστοιχα αν λάβει τιμή μικρότερη της τελικής (αν έχουμε αρνητικό βήμα) τότε η επανάληψη τερματίζεται.
Παρατηρήσεις:
- Η αρχική τιμή, η τελική τιμή και το βήμα μεταβολής μπορεί να είναι αρνητικοί αριθμοί ή θετικοί αριθμοί και δεν είναι απαραίτητο να είναι ακέραιοι.
- Η αρχική και η τελική τιμή μπορεί να είναι μηδέν.
- Αν το βήμα μεταβολής είναι 1 τότε μπορεί να παραληφθεί.
- Το βήμα μεταβολής δεν πρέπει να είναι μηδέν γιατί υπάρχει κίνδυνος μη τερματισμού του αλγορίθμου.
- Αν αρχική τιμή < τελική τιμή τότε:
- Πρέπει το βήμα μεταβολής να είναι θετικό αλλιώς δεν θα τερματίζεται ο αλγόριθμος.
- Η εκτέλεση των εντολών που έπονται του ελέγχου θα σταματήσει όταν ο μετρητής > τελική τιμή.
- Αν αρχική τιμή > τελική τιμή τότε:
- Αν το βήμα μεταβολής είναι θετικό δε θα εκτελεστούν καμία φορά οι εντολές που έπονται της εντολής ελέγχου,
- Αν το βήμα μεταβολής είναι αρνητικό, η εκτέλεση των εντολών που έπονται του ελέγχου θα σταματήσει όταν μετρητής < τελική τιμή.
Υπολογισμός πλήθους επαναλήψεων
Ένας τρόπος να υπολογίσουμε το πλήθος των επαναλήψεων που θα εκτελεσθούν σε μια δομή «ΓΙΑ…ΑΠΟ…ΜΕΧΡΙ…» είναι ο εξής :
(Τελική τιμή – Αρχική τιμή ) DIV ( Βήμα ) + 1 = Πλήθος επαναλήψεων
Η Δομή Επανάληψης "ΟΣΟ"
Σε αρκετές περιπτώσεις ασκήσεων όπου η χρήση επαναλήψεων είναι αναγκαία για την επίλυση του προβλήματος , θα παρατηρήσουμε ότι η δομή επανάληψης «για» δεν θα μπορεί να φανεί χρήσιμη. Αυτές θα είναι οι περιπτώσεις στις οποίες δεν θα γνωρίζουμε το πλήθος των επαναλήψεων που θα εκτελεστούν ή αυτό είναι το ζητούμενο της άσκησης.
Για παράδειγμα όταν η άσκηση ζητά να υπολογίσουμε το άθροισμα 100 τυχαίων αριθμών τότε ξέρουμε ότι θα γίνουν 100 επαναλήψεις και μπορούμε να χρησιμοποιήσουμε τη δομή επανάληψης «για».
Αν όμως η άσκηση ζητά να «δέχεται» ο υπολογιστής τυχαίους αριθμούς από το πληκτρολόγιο ( θα τους δίνει ο χρήστης) μέχρι να «δεχθεί» σαν είσοδο τον αριθμό 79, τότε δεν γνωρίζουμε από την αρχή πόσες επαναλήψεις θα συμβούν μέχρι να δοθεί ο αριθμός 79 διότι οι αριθμοί δίνονται με τυχαία σειρά. Σε αυτές τις περιπτώσεις τη λύση μας δίνει η δομή επανάληψης «όσο».
Αξίζει να σημειώσουμε ότι η δομή επανάληψης «όσο» μπορεί να δώσει λύση σε οποιαδήποτε άσκηση στην οποία γίνεται χρήση επαναληπτικών διαδικασιών είτε γνωρίζουμε, είτε όχι το πλήθος των επαναλήψεων εξ αρχής. Ας δούμε πως συντάσσουμε μια επανάληψη χρησιμοποιώντας αυτή τη δομή.
ΟΣΟ ( ΛΟΓΙΚΗ ΣΥΝΘΗΚΗ ) ΕΠΑΝΑΛΑΒΕ
{ ΟΜΑΔΑ ΕΝΤΟΛΩΝ }
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
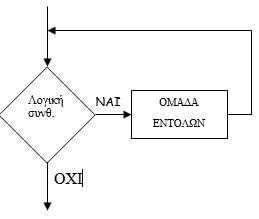
Η διαγραμματική αναπαράσταση της δομής επανάληψης «ΟΣΟ…ΕΠΑΝΑΛΑΒΕ» , είναι η παρακάτω :
Για παράδειγμα όταν η άσκηση ζητά να υπολογίσουμε το άθροισμα 100 τυχαίων αριθμών τότε ξέρουμε ότι θα γίνουν 100 επαναλήψεις και μπορούμε να χρησιμοποιήσουμε τη δομή επανάληψης «για».
Αν όμως η άσκηση ζητά να «δέχεται» ο υπολογιστής τυχαίους αριθμούς από το πληκτρολόγιο ( θα τους δίνει ο χρήστης) μέχρι να «δεχθεί» σαν είσοδο τον αριθμό 79, τότε δεν γνωρίζουμε από την αρχή πόσες επαναλήψεις θα συμβούν μέχρι να δοθεί ο αριθμός 79 διότι οι αριθμοί δίνονται με τυχαία σειρά. Σε αυτές τις περιπτώσεις τη λύση μας δίνει η δομή επανάληψης «όσο».
Αξίζει να σημειώσουμε ότι η δομή επανάληψης «όσο» μπορεί να δώσει λύση σε οποιαδήποτε άσκηση στην οποία γίνεται χρήση επαναληπτικών διαδικασιών είτε γνωρίζουμε, είτε όχι το πλήθος των επαναλήψεων εξ αρχής. Ας δούμε πως συντάσσουμε μια επανάληψη χρησιμοποιώντας αυτή τη δομή.
ΟΣΟ ( ΛΟΓΙΚΗ ΣΥΝΘΗΚΗ ) ΕΠΑΝΑΛΑΒΕ
{ ΟΜΑΔΑ ΕΝΤΟΛΩΝ }
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
Η διαγραμματική αναπαράσταση της δομής επανάληψης «ΟΣΟ…ΕΠΑΝΑΛΑΒΕ» , είναι η παρακάτω :
Παρατηρήσεις στη δομή επανάληψης «όσο»
- Η επανάληψη στην δομή αυτή συνεχίζεται όσο ισχύει η λογική συνθήκη, όταν η λογική συνθήκη γίνει ψευδής τότε τερματίζεται η επανάληψή μας.
- Η δομή επανάληψης «όσο» μπορεί να λειτουργήσει τόσο με τη χρήση μετρητή όσο και χωρίς αυτόν.
- Όταν γνωρίζουμε πόσες φορές θα γίνει η επανάληψη η χρήση μετρητή είναι απαραίτητη διότι αυτός θα ρυθμίσει πότε θα τερματιστεί η επανάληψη. Σε αυτή την περίπτωση ο μετρητής βρίσκεται και στη λογική συνθήκη.
- Όταν το ζητούμενο είναι να μετρήσουμε πόσες φορές θα πραγματοποιηθεί η επανάληψη τότε ο μετρητής δεν βρίσκεται στη λογική συνθήκη αλλά αλλάζει τιμή κάθε φορά που εκτελείται η επανάληψη.
- Όταν δεν γνωρίζουμε πόσες φορές θα γίνει η επανάληψη , αλλά ούτε και είναι ζητούμενο κάτι τέτοιο, τότε δεν χρησιμοποιούμε καθόλου μετρητή.
- Ιδιαίτερη προσοχή πρέπει να δοθεί στη λογική συνθήκη της επανάληψης. Δηλαδή πρέπει να είμαστε σίγουροι ότι η λογική συνθήκη θα τερματίζεται κάποια στιγμή διότι σε διαφορετική περίπτωση η επανάληψη θα εκτελείται απ’ άπειρον (Ατέρμων βρόγχος). Κάτι τέτοιο είναι ένα σοβαρό λογικό λάθος. Η λογική συνθήκη σε αυτή τη δομή επανάληψης μας παρέχει την «ελευθέρια» να ρυθμίσουμε την επανάληψη όπως ακριβώς επιθυμούμε. Επίσης αξίζει να σημειωθεί ότι η δομή της επανάληψης αυτής μπορεί να μην εκτελεστεί ούτε μια φορά. Όπως καταλαβαίνουμε, αν η λογική συνθήκη είναι ψευδής εξ αρχής τότε η δομή αυτή δεν θα εκτελεστεί ούτε μια φορά.
Η Δομή Επανάληψης "Μέχρις_Οτου"
Η δομή επανάληψης «μέχρις_ότου» είναι η τρίτη δομή επανάληψης την οποία θα μελετήσουμε. Η δομή αυτή παρουσιάζει αρκετές ομοιότητες με τη δομή επανάληψης «όσο» αλλά έχει και κάποιες σημαντικές διαφορές.
Η χρήση της δομής αυτής μας επιτρέπει να λύνουμε προβλήματα στα οποία δεν γνωρίζουμε εκ των προτέρων πόσες επαναλήψεις θα γίνουν , πρέπει όμως να είμαστε σίγουροι ότι η επανάληψη θα εκτελεστεί τουλάχιστον μια φορά, αν δεν είμαστε απόλυτα βέβαιοι, τότε θα επιλέγουμε την δομή επανάληψης «όσο» ως καταλληλότερη.
Ας δούμε πιο αναλυτικά πως συντάσσεται η δομή αυτή και πως τη χρησιμοποιούμε:
ΑΡΧΗ_ΕΠΑΝΑΛΗΨΗΣ
{ ΟΜΑΔΑ ΕΝΤΟΛΩΝ }
ΜΕΧΡΙΣ_ΟΤΟΥ (ΛΟΓΙΚΗ ΣΥΝΘΗΚΗ
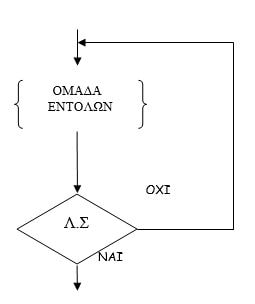
Η διαγραμματική αναπαράσταση της δομής επανάληψης "Μέχρις_Οτου" είναι η εξής :
Η χρήση της δομής αυτής μας επιτρέπει να λύνουμε προβλήματα στα οποία δεν γνωρίζουμε εκ των προτέρων πόσες επαναλήψεις θα γίνουν , πρέπει όμως να είμαστε σίγουροι ότι η επανάληψη θα εκτελεστεί τουλάχιστον μια φορά, αν δεν είμαστε απόλυτα βέβαιοι, τότε θα επιλέγουμε την δομή επανάληψης «όσο» ως καταλληλότερη.
Ας δούμε πιο αναλυτικά πως συντάσσεται η δομή αυτή και πως τη χρησιμοποιούμε:
ΑΡΧΗ_ΕΠΑΝΑΛΗΨΗΣ
{ ΟΜΑΔΑ ΕΝΤΟΛΩΝ }
ΜΕΧΡΙΣ_ΟΤΟΥ (ΛΟΓΙΚΗ ΣΥΝΘΗΚΗ
Η διαγραμματική αναπαράσταση της δομής επανάληψης "Μέχρις_Οτου" είναι η εξής :
ΠΑΡΑΤΗΡΗΣΕΙΣ:
- Στη παραπάνω δομή έχουμε τη λογική συνθήκη στο τέλος, σε αντίθεση με την δομή επανάληψης «όσο» στην οποία η λογική συνθήκη ήταν στην αρχή της επανάληψης.
- Η λογική συνθήκη σε αυτή την περίπτωση είναι συνθήκη τερματισμού και όχι συνέχισης της επανάληψης. Παρατηρούμε ότι όσο η λογική συνθήκη είναι ψευδής η επανάληψη συνεχίζεται, ενώ όταν η λογική συνθήκη γίνει αληθής η επανάληψη τερματίζεται.
- Μεγάλη προσοχή πρέπει να δοθεί στο γεγονός ότι σε αυτή τη δομή επανάληψης η ομάδα εντολών ( όποια κι αν είναι αυτή ) θα εκτελεστεί τουλάχιστον μια φορά. Αυτό συμβαίνει γιατί η λογική συνθήκη είναι στο τέλος της δομής έτσι για να «φτάσει» ο αλγόριθμος σε αυτή θα εκτελέσει την ομάδα εντολών τουλάχιστον μια φορά. Αυτό είναι και το πιο λεπτό σημείο το οποίο πρέπει να προσέχουμε σε αυτή τη δομή: αν η ομάδα εντολών ΔΕΝ πρέπει να εκτελεστεί τότε δεν χρησιμοποιούμε τη δομή επανάληψης «μέχρις_ότου» γιατί κινδυνεύουμε να υποπέσουμε σε λογικό λάθος.
- Η δομή επανάληψης «μέχρις_ότου» μπορεί να δώσει λύση σε όλα σχεδόν τα προβλήματα που απαιτούν χρήση επανάληψης. Υπάρχει μόνο ένας περιορισμός : Πρέπει να είμαστε απολύτως σίγουροι ότι η ομάδα εντολών θα εκτελεστεί ΤΟΥΛΑΧΙΣΤΟΝ μια φορά, αν δεν είμαστε σίγουροι για αυτό τότε θα είναι καλύτερα να χρησιμοποιήσουμε την δομή επανάληψης «όσο».