Γενικά 

Το δεύτερο είδος πινάκων που θα μελετήσουμε είναι οι δισδιάστατοι πίνακες. Σε αυτού του είδους τους πίνακες έχουμε την ευχέρεια διαχείρισης μεγαλύτερου πλήθους δεδομένων από ότι στους μονοδιάστατους. Ένας δισδιάστατος πίνακας   χαρακτηρίζεται από το πόσες γραμμές και πόσες στήλες έχει. Επίσης οι λειτουργίες που μπορούμε να εκτελέσουμε σε ένα τέτοιο πίνακα είναι παρόμοιες με τις λειτουργίες σε μονοδιάστατο πίνακα μόνο που εδώ πλέον θα μπορούμε να επιλέγουμε αν θέλουμε να επεξεργαστούμε όλα τα στοιχεία του πίνακα ή τα στοιχεία κάθε γραμμής ή κάθε στήλης ξεχωριστά.
 
Όταν αναφερόμαστε σε ένα δισδιάστατο πίνακα θα γράφουμε το όνομά του και μέσα στην αγκύλη που ακολουθεί θα αναφερόμαστε στις γραμμές και τις στήλες του αντίστοιχα. 

Οι γραμμές και οι στήλες σε δισδιάστατο πίνακα Π [3,4]

Αν ονομάσουμε Π τον παραπάνω πίνακα τότε θα τον δηλώναμε ως εξής : Π[3,4]
Γενικότερα γράφουμε : ΟΝΟΜΑ [ ΓΡΑΜΜΕΣ , ΣΤΗΛΕΣ] 

Βασικές Μεθοδολογίες 
​
1. Καταχώρηση στοιχείων σε δισδιάστατο πίνακα . "Γέμισμα" του πίνακα με στοιχείαt.

Στην περίπτωση του δισδιάστατου πίνακα η διαδικασία που ακολουθούμε προκειμένου να τον «γεμίσουμε» ακολουθεί την ίδια φιλοσοφία, η διαφορά είναι ότι στο δισδιάστατο πίνακα θα χρησιμοποιούμε δύο επαναλήψεις ( η μια πάντα αναφέρεται στης γραμμές και η άλλη στις στήλες του πίνακα).

Έστω ότι έχουμε ένα πίνακα Π με Γ γραμμές και Σ στήλες , δηλαδή έχουμε τον Π[Γ,Σ] . Το πίνακα αυτό μπορούμε να τον γεμίσουμε είτε κατά γραμμή είτε κατά στήλη. 

Γέμισμα του πίνακα Π[Γ,Σ] κατά γραμμή

ΓΙΑ i ΑΠΟ 1 ΜΕΧΡΙ Γ
     ΓΙΑ J ΑΠΟ 1 ΜΕΧΡΙ Σ
          ΓΡΑΨΕ 'ΔΩΣΕ ΤΟ ΣΤΟΙΧΕΙΟ'
          ΔΙΑΒΑΣΕ Π[i,J]
     ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
​ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ

Γέμισμα του πίνακα Π[Γ,Σ] κατά στήλη

ΓΙΑ j ΑΠΟ 1 ΜΕΧΡΙ Σ
     ΓΙΑ i ΑΠΟ 1 ΜΕΧΡΙ Γ
          ΓΡΑΨΕ 'ΔΩΣΕ ΤΟ ΣΤΟΙΧΕΙΟ'
          ΔΙΑΒΑΣΕ Π[i,J]
     ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
​ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ

---

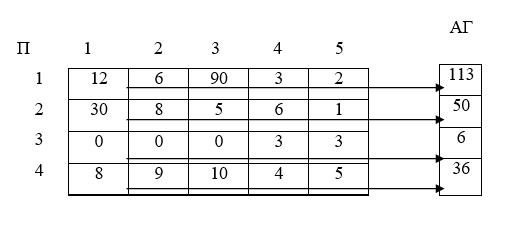
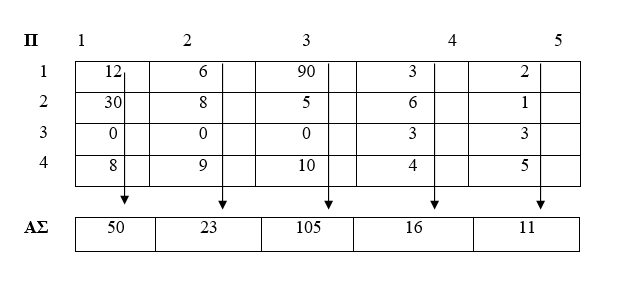
2. Εύρεση Αθροίσματος σε δισδιάστατο πίνακα

Όπως το γέμισμα έτσι και οι υπόλοιπες λειτουργίες σε ένα δισδιάστατο πίνακα μπορούν να γίνουν είτε κατά γραμμή, είτε κατά στήλη είτε σε όλο τον πίνακα συνολικά.. Το πώς θα επεξεργαστούμε τον πίνακα καθορίζεται κάθε φορά από τη σειρά με την οποία τοποθετούμε τις επαναλήψεις οι οποίες αναφέρονται στις γραμμές και τις στήλες ενός πίνακα δυο διαστάσεων.

Εύρεση Αθροίσματος κατά Γραμμή : 
​
       Για  i από 1 μέχρι Γ
             ΑΓ[ i ] <-- 0
             Για j από 1 μέχρι Σ
                  ΑΓ [ i ] <-- ΑΓ[ i ] + Π [ i, j ]
             Τέλος_επανάληψης
       Τέλος_επανάληψης 

Εύρεση αθροίσματος κατά γραμμή σε δισδιάστατο πίνακα Π [4,5]

Εύρεση Αθροίσματος κατά Στήλη : 

​       Για  j από 1 μέχρι Σ
             ΑΣ [ j ] <--0
             Για i από 1 μέχρι Γ
                   ΑΣ [ j ] <-- ΑΣ [ j ] + Π [ i, j ]
             Τέλος_επανάληψης
         Τέλος_επανάληψης 

Εύρεση αθροίσματος κατά στήλη σε δισδιάστατο πίνακα Π [4,5]

Εύρεση του Αθροίσματος όλων των στοιχείων του πίνακα:

Η περίπτωση αυτή είναι ευκολότερη από τις προηγούμενες δυο , διότι δεν χρειάζεται να χρησιμοποιήσουμε βοηθητικό πίνακα αλλά απλά μια μεταβλητή.
​
        S <-- 0
        Για  i από 1 μέχρι Γ
               Για j από 1 μέχρι Σ
                     S <-- S + Π [ i, j ]
               Τέλος_επανάληψης
        Τέλος_επανάληψης

---

3. Εύρεση του Μέσου Όρου των στοιχείων ενός δισδιάστατου πίνακα
​

Ο υπολογισμός του μέσου όρου ενός δισδιάστατου πίνακα μπορεί να «ζητηθεί» με τρεις τρόπους: 
​                         α) υπολογισμός του μέσου όρου κάθε γραμμής του πίνακα,
                         β) υπολογισμός του μέσου όρου κάθε στήλης του πίνακα, και
                         γ) υπολογισμός του μέσου όρου όλων των στοιχείων του πίνακα.
Βασική προϋπόθεση για την εύρεση ενός μέσου όρου είναι να γνωρίζουμε το άθροισμα των στοιχείων, των οποίων επιθυμούμε να υπολογίσουμε το μέσο όρο, και να το διαιρέσουμε με το πλήθος τους.

Εύρεση Μέσου Όρου κατά γραμμή : 

     Για  i από 1 μέχρι Γ
           S <--0
           Για j από 1 μέχρι Σ
                S <-- S + Π [ i, j ]
           Τέλος_επανάληψης
           ΜΓ [ i ] <-- S/ Σ
      Τέλος_επανάληψης 

Εύρεση Μέσου Όρου κατά στήλη : 

         Για  j από 1 μέχρι Σ
               S <--0
               Για i από 1 μέχρι Γ
                    S <-- S + Π [ i, j ]
               Τέλος_επανάληψης
               ΜΣ [ j ] <-- S / Γ
          Τέλος_επανάληψης 

Εύρεση Γενικού Μέσου Όρου: 

            S <-- 0
            Για  i από 1 μέχρι Γ
                  Για j από 1 μέχρι Σ
                         S <-- S + Π [ i, j ]
                  Τέλος_επανάληψης
             Τέλος_επανάληψης
             Μ <-- S / ( Γ * Σ )

---

4. Εύρεση Μέγιστου (max) ή Ελάχιστου (min) στοιχείου σε δισδιάστατο πίνακα

​ Ο τρόπος εύρεσης του μέγιστου ή ελάχιστου στοιχείου ενός δισδιάστατου πίνακα δεν διαφέρει από εκείνο που χρησιμοποιήσαμε για την αντίστοιχη δουλειά σε μονοδιάστατο πίνακα. Δηλαδή θέτουμε το πρώτο στοιχείο του πίνακα ως μέγιστο και ακολουθεί η σύγκρισή του με τα υπόλοιπα στοιχεία του πίνακα. Όπως και στις προηγούμενες ενέργειες που μελετήσαμε έτσι και εδώ η εύρεση μέγιστου ή ελάχιστου μπορεί να γίνει κατά γραμμή, κατά στήλη ή σε όλο τον πίνακα.

Εύρεση Ελάχιστου (min) κατά γραμμή:

            Για  i από 1 μέχρι Γ
                   min [i] <-- Π [ i , 1]
                   Για j από 1 μέχρι Σ
                        Αν Π [ i , j ]< min τότε
                              min<--Π[ i , j ]
                        τέλος_αν
                   τέλος_επανάληψης
            τέλος_επανάληψης

Εύρεση Μέγιστου (max) κατά στήλη : 

            Για j από 1 μέχρι Σ
                  max [ j ] <-- Π [ 1, j ]
                  Για i από 1 μέχρι Γ
                       Αν Π[ i,j] > max [ j ] τότε
                              max [ j ] <-- Π [ i, j ]
                        Τέλος_αν
                   τέλος_επανάληψης
            τέλος_επανάληψης

Εύρεση Μέγιστου (max) σε όλο τον πίνακα: 

            max <-- Π [ 1,1]
            Για i από 1 μέχρι Γ
                        Για j από 1 μέχρι Σ
                                    Αν Π [ i , j ] > max τότε
                                                max <-- Π [ i , j]
                                    τέλος_αν
                        τέλος_επανάληψης
            τέλος_επανάληψης

---

Παράδειγμα :
Να πραγματοποιηθεί πρόγραμμα το οποίο θα δέχεται τα ονόματα 40 μαθητών και τους βαθμούς τους σε 6 μαθήματα και θα υπολογίζει :
Α. Το μέσο όρο του κάθε μαθητή,
Β. Το μέσο όρο του κάθε μαθήματος , και
Γ. Θα εμφανίζει το όνομα του καλύτερου μαθητή.
​

ΠΡΟΓΡΑΜΜΑ ΜΑΘΗΤΕΣ
ΜΕΤΑΒΛΗΤΕΣ
                ΑΚΕΡΑΙΕΣ: Ι, J , Θ
                ΠΡΑΓΜΑΤΙΚΕΣ: Π [ 40 , 6 ] , Μ[40] , ΜΣ [ 6 ]
                ΧΑΡΑΚΤΗΡΕΣ: Α[40]
ΑΡΧΗ
 
ΓΙΑ Ι ΑΠΟ 1 ΜΕΧΡΙ 40
                ΓΡΑΨΕ ' ΔΩΣΕ ΤΟ ΟΝΟΜΑ ΤΟΥ’, Ι, ’ου ΜΑΘΗΤΗ’
                ΔΙΑΒΑΣΕ Α[Ι]
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
ΓΙΑ Ι ΑΠΟ 1 ΜΕΧΡΙ 40
                ΓΙΑ J ΑΠΟ 1 ΜΕΧΡΙ 6
                                ΓΡΑΨΕ ‘ ΔΩΣΕ ΤΟ ΒΑΘΜΟ ΤΟΥ’, Ι ,’ ου ΜΑΘΗΤΗ ΣΤΟ ‘, J ,’ο ΜΑΘΗΜΑ’
                                ΔΙΑΒΑΣΕ Π[ I , J ]
                ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
 
!ΥΠΟΛΟΓΙΣΜΟΣ ΜΕΣΟΥ ΟΡΟΥ ΚΑΘΕ ΜΑΘΗΤΗ
ΓΙΑ Ι ΑΠΟ 1 ΜΕΧΡΙ 40
                Μ[ Ι ]<--0
                ΓΙΑ J ΑΠΟ 1 ΜΕΧΡΙ 6
                                Μ [ Ι ]<-- Μ[ Ι ]+   Π [Ι, J]
                ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
                Μ [ Ι ]<-- Μ [ Ι ] / 6
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
ΓΙΑ Ι ΑΠΟ 1 ΜΕΧΡΙ 40
                ΓΡΑΨΕ ‘ Ο ΜΕΣΟΣ ΟΡΟΣ ΤΟΥ :’, Α[ Ι ] ‘, ΕΙΝΑΙ: ‘, Μ [ Ι ]
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ

! ΥΠΟΛΟΓΙΣΜΟΣ ΜΕΣΟΥ ΟΡΟΥ ΚΑΘΕ ΜΑΘΗΜΑΤΟΣ
ΓΙΑ J ΑΠΟ 1 ΜΕΧΡΙ 6
                ΜΣ [ J ] <--0
                ΓΙΑ Ι ΑΠΟ 1 ΜΕΧΡΙ 40
                                ΜΣ [ J ] <-- ΜΣ[ J ] + Π [ Ι, J ]
                ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
                ΜΣ[ J ] <-- ΜΣ [ J ] / 40
ΤΕΛΟΣ_ΕΠΑΝΛΗΨΗΣ
ΓΙΑ  J ΑΠΟ 1 ΜΕΧΡΙ 6
                ΓΡΑΨΕ ‘ Ο ΜΕΣΟΣ ΟΡΟΣ ΤΟΥ ‘, J ,’ ΟΥ ΜΑΘΗΜΑΤΟΣ ΕΙΝΑΙ :’, ΜΣ[ J ]
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
 
! ΕΥΡΕΣΗ ΤΟΥ ΟΝΟΜΑΤΟΣ ΤΟΥ ΚΑΛΥΤΕΡΟΥ ΜΑΘΗΤΗ.
! ΚΑΛΥΤΕΡΟΣ ΜΑΘΗΤΗΣ ΕΙΝΑΙ ΑΥΤΟΣ ΠΟΥ ΕΧΕΙ ΤΟ ΜΕΓΑΛΥΤΕΡΟ ΜΕΣΟ ΟΡΟ.
ΜΑΧ <-- Μ [ 1 ]
Θ <--1
ΓΙΑ Ι ΑΠΟ 1 ΜΕΧΡΙ 40
                ΑΝ Μ [ Ι ] > ΜΑΧ ΤΟΤΕ
                                ΜΑΧ <-- Μ [ Ι ]
                                Θ <-- Ι
                ΤΕΛΟΣ_ΑΝ
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
ΓΡΑΨΕ ‘ ΚΑΛΥΤΕΡΟΣ ΜΑΘΗΤΗΣ ΕΙΝΑΙ Ο : ‘, Α [ Θ ]
ΤΕΛΟΣ_ΠΡΟΓΡΑΜΜΑΤΟΣ